Proof for a Post a While Back

In a post a while back, I mentioned that I’d found that:

$1-\frac{1}{\sqrt[k]{2}}\approx\frac{\ln 2}{k}$

for sufficiently large k, which relates to finding the median of the minimum of a set of k independent, identically-distributed random variables. I didn’t have a proof at the time, but I’ve thought of a very simple “proof”:

$(1-\frac{1}{x})^x \approx \frac{1}{e}$ for large x.

$1-\frac{1}{x} \approx \frac{1}{\sqrt[x]{e}}$

$1-\frac{1}{\sqrt[x]{e}} \approx \frac{1}{x}$

$1-\frac{1}{\sqrt[k]{e^{\ln 2}}} \approx \frac{\ln 2}{k}; x = \frac{k}{\ln 2}$

$1-\frac{1}{\sqrt[k]{2}} \approx \frac{\ln 2}{k}$

It’s by no means rigorous, as things that are “approximately equal” put through certain transformations can result in values that are not even close, but it seems to check out in this case.

~ by Neil Dickson on December 14, 2009.

Posted in Math

2 Responses to “Proof for a Post a While Back”

Actually, if you perform a series expansion of the LHS of the equation around x = Infinity you will see that the first term is ln2/k. The second one is (ln2)^2/(2k^2), which for k very large is much smaller than the first term. In principle, you are looking at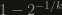 $1 - 2^{-1/k}$ for k –> Infinity. You could also look at 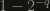$1 - 2^{-q}$ for q –> 0 which is easier to treat. Will reply to your email later…

Helmut said this on December 27, 2009 at 9:16 pm | Reply
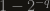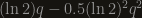Ah yes, of course, the Taylor series for $1-2^{-q}$ about $q=0$ starts with $(\ln 2)q - 0.5 (\ln 2)^2 q^2$ . Thanks! 🙂

Neil Dickson said this on December 28, 2009 at 4:04 am | Reply